Đề cương ôn tập môn Hình học Lớp 9 (Dành cho học sinh TB, Yếu) - Tuần 24 đến 31 - Năm học 2019-2020 - Tôn Trần Thái Hậu

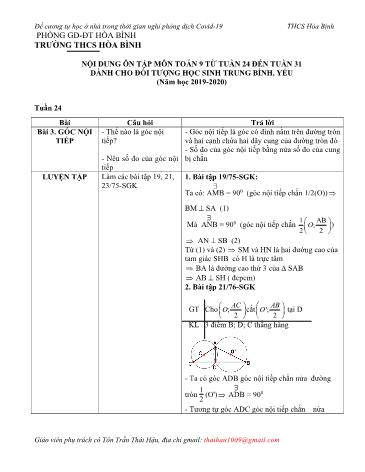
 Đề cương tự học ở nhà trong thời gian nghỉ phòng dịch Covid-19 THCS Hòa Bình 
 
 AC 0
 đường tròn O; ADC = 90 
 2 
   
 Mà BDC = ADB + ADC 
 
 BDC = 900 +900 = 1800 
 3 điểm B, D, C thẳng hàng (đpcm) 
 3. Bài tập 23/76-SGK 
 a) Trường hợp điểm M nằm trong (O) 
 - Xét A M C và D M B 
  
 Có AMC = BMD (2 góc đối đỉnh) 
  
 AMC=MBD (2 góc n/t cùng chắn AD) 
 S (g . g) 
 MAMD
 = 
 MCMB
 MA.. MB MC MD (đpcm) 
 b) Trường hợp điểm M nằm ngoài (O): 
 - Xét A M D và CM B 
 
 Có M (góc chung) 
  
 ADM = MDC (2 góc n/t cùng chắn AC) 
 (g . g) 
 MA.MB =MC.MD 
 Tuần 25: 
 Bài Câu hỏi Trả lời 
 Bài 4. GÓC TẠO - Nêu khái niệm về góc Góc tạo bởi tia tiếp tuyến và dây cung là góc có 
 BỞI TIẾP tạo bởi tia tiếp tuyến và đỉnh nằm trên đường tròn một cạnh là tia tiếp 
TUYẾN VÀ DÂY dây cung tuyến, cạnh còn lại chứa một dây cung của đường 
 CUNG tròn. 
 - Tâm đường tròn nằm trên cạnh chứa dây của 
 - Phát biểu thành định lý góc. 
 về số đo của góc tạo bởi - Tâm đường tròn nằm trong góc. 
 tia tiếp tuyến và dây - Tâm đường tròn nằm ngoài góc. 
 cung và số đo của cung 
 bị chắn. 
Giáo viên phụ trách cô Tôn Trần Thái Hậu, địa chỉ gmail: thaihau1009@gmail.com 
 Đề cương tự học ở nhà trong thời gian nghỉ phòng dịch Covid-19 THCS Hòa Bình 
 Tuần 26: 
 Bài Câu hỏi Trả lời 
 Bài 5. GÓC CÓ 
ĐỈNH Ở TRONG Nêu khái niệm về góc Góc có đỉnh bên trong đường tròn là góc có đỉnh 
 ĐƯỜNG TRÒN. có đỉnh bên trong đường nằm bên trong đường tròn, góc có đỉnh ở ngoài 
 GÓC CÓ ĐỈNH tròn, góc có đỉnh ở đường tròn là góc có đỉnh nằm bên ngoài đường 
 Ở NGOÀI ngoài đường tròn tròn 
 ĐƯỜNG TRÒN 
 LUYỆN TẬP Cho đường tròn (O) và 
 hai dây AB, AC. Gọi M, 
 N lần lượt là điểm chính 
 giữa của cung AB và 
 cung AC. Đường thẳng 
 MN cắt dây AB tại E và 
 cắt dây AC tại H. 
 Chứng minh tam giác Theo định lí góc có đỉnh ở bên trong đường tròn, 
 AEH là tam giác cân. ta có: 
 ˆAHM = (sđ⁀AM + sđ⁀NC):2 
 AEN^ = sđ⁀MB−sđ⁀AN/2 
 Mà theo giả thiết: ⁀AM = ⁀MB, ⁀NC = 
 ⁀AN. 
 Suy ra ˆAHM = ˆAEN 
 Cho đường tròn (O) và Do đó tam giác AEH cân tại A. (đpcm) 
 hai dây AB, AC bằng 
 nhau. Trên cung nhỏ 
 AC lấy một điểm M. 
 Gọi S là giao điểm của 
 AM và BC. Chứng 
 minh ˆASC =ˆMCA^. 
 Ta có ˆASC = sđ⁀AB−sđ⁀MC/2 (1) (theo định 
 lí góc có đỉnh ở ngoài đường tròn) 
 Ta cũng có ˆMCA = sđ⁀AM/2 (góc nội tiếp 
 chắn cung AM) 
 Hay ˆMCA = sđ⁀AC−sđ⁀MC/2 (2) 
 Mặt khác ta có AB = AC (gt) 
 Suy ra ⁀AB = ⁀AC (3) 
 Từ (1), (2) và (3) suy ra ˆASC = ˆMCA (đpcm). 
 Trên một đường tròn, 
 lấy liên tiếp ba cung 
 AC, CD, DB sao cho 
 sđ⁀AC = sđ⁀CD = 
 sđ⁀DB = 600. Hai 
 đường thẳng AC và BD 
Giáo viên phụ trách cô Tôn Trần Thái Hậu, địa chỉ gmail: thaihau1009@gmail.com 
 Đề cương tự học ở nhà trong thời gian nghỉ phòng dịch Covid-19 THCS Hòa Bình 
 1350 không đổi. Vậy quỹ tích điểm I là cung 
 chứa góc 1350 dựng trên đoạn BC. 
 2. Bài 46/86-sgk 
 - Dựng đoạn AB = 3cm ( dùng thước có chia 
 khoảng) 
 - Dựng góc xAB = 550 
 - Dựng tia Ay vuông góc với Ax 
 - Dựng đường trung trực d của đoạn AB. Gọi O 
 là giao điểm của d và Ay 
 - Dựng đường tròn tâm O, bán kính OA; AmB là 
 cung chứa góc 550 dựng trên đoạn AB = 3cm 
 Tuần 28: 
 Bài Câu hỏi Trả lời 
 Bài 7. TỨ GIÁC Thế nào là tứ giác nội Tứ giác có 4 đỉnh nằm trên đường tròn được gọi 
 NỘI TIẾP tiếp đường tròn ? là tứ giác nội tiếp đường tròn. 
 Trong một tứ giác nội tiếp tổng hai góc đối bằng 
 Nêu định lí về tứ giác 1800 
 nội tiếp 
 LUYỆN TẬP 1. Bài tập 56/89-sgk: 
 Cho ho HS làm bài tập 
 56, 58, 59/89, 90-sgk 
 0 
 Xét ∆EAD có: E + A + D1 = 180
 0
 Xét ∆FAB có: F + + B1 = 180 
 + + + + + = 3600. 
 Nên : 2 A = 1200 A = 600. 
 0 0 0
 Do đó : C1 = 120 ; B1 = 100 ; D1 = 80 . 
 2. Bài tập 58/90-sgk: 
 a) Ta có: ACB = 600 = ABC 
Giáo viên phụ trách cô Tôn Trần Thái Hậu, địa chỉ gmail: thaihau1009@gmail.com 
 Đề cương tự học ở nhà trong thời gian nghỉ phòng dịch Covid-19 THCS Hòa Bình 
 Tuần 30: 
 Bài Câu hỏi Trả lời 
 LUYỆN TẬP 1. Bài tập 73/96-sgk: 
 Ta có: C 40000km 
 Cho ho HS làm bài tập C 40000
 C = 2 R => R = 6369 
 73, 74, 75/96-sgk 22 
 2. Bài tập 74/96-sgk: 
 0
 1201 
 Ta có : n0 = 20001’ = 
 60 
 C 40000km => R 6369km 
 1201
 Rn .6396.
 l 60 2233km 
 180180
 3. Bài tập 75/96-sgk: 
 .OM .n
 Ta có : l MA = 
 180
 .O' M.2n .OM .n
 l MB = = 
 180 180
 Vậy : l = l MB 
 §10. DIỆN TÍCH Nêu công thức tính diện Diện tích S của một hình tròn bán kính R được 
 HÌNH TRÒN, tích hình tròn (nêu tên tính theo công thức: 
 HÌNH QUẠT các đại lượng có mặt S = π.R2 
 TRÒN trong công thức) 
 Nêu công thức tính hình S là diện tích hình quạt có bán kính R, cung n0. 
 2
 quạt tròn (nêu tên các Sq = πR n/360 hay Sq = lR/2 (l là độ dài cung có 
 đại lượng có mặt trong số đo n0) 
 công thức) 
 Tuần 31: 
 Bài Câu hỏi Trả lời 
 LUYỆN TẬP Cho ho HS làm bài tập 1.Bài tập 85/100-sgk: 
 85, 86/100-sgk 
Giáo viên phụ trách cô Tôn Trần Thái Hậu, địa chỉ gmail: thaihau1009@gmail.com 
 Đề cương tự học ở nhà trong thời gian nghỉ phòng dịch Covid-19 THCS Hòa Bình 
 5p
 = (cm2) 
 18
 Hình 71: S = 32 - p (1,5)2 
 = 9 – 2,25 p (cm2) 
 ÔN TẬP Cho ho HS làm bài tập 1. Bài tập 95/105-sgk 
 CHƯƠNG III 95, 97/105-sgk 
 (T2) 
 a) Ta có: D AMH D BND 
 0
 ( AMH = B N D = 90 ; H1 = H2 ) 
 Þ A1 = B1 . Nên : C D C= E (theo tính chất góc 
 nội tiếp). Vậy : CD = CE (tính chất liên hệ giữa 
 cung và dây) 
 b) D BHD có BB12= (C D C= E ) và 
 BC^ HDÞ BHD cân tại B 
 c) BHD cân tại B và BC HD nên BC là 
 đường trung trực của HD. 
 Vậy: CH = CD 
 2. Bài tập 97/105-sgk 
 a) Ta có BAC = 900 (gt) BDC = 900 (góc nội tiếp 
 chắn nửa đường tròn) 
 BACBDC==900 . Vậy ABCD nội tiếp đường 
 tròn đường kính BC 
 b) ABDACD= (cùng chắn AD của đường tròn 
 đường kính BC) 
 c) ADBACB= (cùng chắn AB của đường tròn 
 đường kính BC) 
 ADB= SCA (cùng phụ với SDM )Þ ACB= SCA. 
 Vậy CA là phân giác SCB . 
 Hòa Bình, ngày 22 tháng 3 năm 2020 
 GVBM 
 Tôn Trần Thái Hậu 
Giáo viên phụ trách cô Tôn Trần Thái Hậu, địa chỉ gmail: thaihau1009@gmail.com